Introduction: What is Bayes’ Theorem? 🤔
In the world of probability theory, few concepts are as powerful and widely applicable as Bayes’ theorem. Named after Thomas Bayes, an 18th-century statistician, Bayes’ theorem helps us calculate the probability of an event based on prior knowledge of conditions related to the event. It’s a key tool in understanding conditional probability, which is the likelihood of an event occurring given that another event has already happened.
In this guide, we’ll break down Bayes’ theorem into simple terms, explain its formula, and show how it’s applied to real-world problems. Whether you’re a beginner trying to grasp the basics or someone looking for practical examples, this blog will make Bayes’ theorem crystal clear.
The Formula: Breaking Down Bayes' Theorem 🔢
Bayes’ theorem is expressed mathematically as:
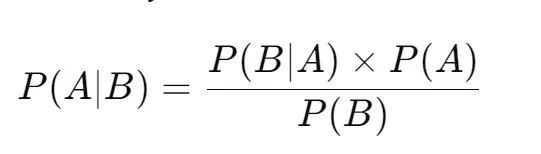
Where:
-
P(A|B): The posterior probability, or the probability of event A occurring given that event B is true.
-
P(B|A): The likelihood, or the probability of event B occurring given that A is true.
-
P(A): The prior probability of event A occurring, independent of B.
-
P(B): The marginal likelihood or the total probability of event B occurring.
Don’t worry if this formula looks intimidating at first! We’ll break it down into simple terms and use examples to show how it works.
Step-by-Step Breakdown of Bayes’ Theorem 📖
Let’s simplify this:
-
Prior probability P(A)P(A)P(A): This is what we know before any new evidence comes in. For example, if we’re interested in the probability that someone has a certain disease, this would be the general likelihood of having the disease before any test results come in.
-
Likelihood P(B∣A)P(B|A)P(B∣A): This is how likely the new evidence (B) is if our hypothesis (A) is true. For example, if we are given a positive test result for the disease, this would be the likelihood of getting that positive result if the person actually has the disease.
-
Posterior probability P(A∣B)P(A|B)P(A∣B): This is what we’re trying to figure out—the probability of A (having the disease) given the new evidence B (the test result). This is the updated probability after combining prior knowledge with the new evidence.
Bayes’ theorem allows us to update our initial beliefs in light of new evidence!
Example: Medical Diagnosis 🏥
Imagine you’re testing for a rare disease that affects 1% of the population. A doctor tells you that the test for this disease is 99% accurate in detecting it (true positive rate), but it also has a 5% false positive rate (where the test says you have the disease even when you don’t).
Now, let’s calculate the probability that you actually have the disease if you test positive.
Step 1: Identify the values we know.
-
P(Disease) = 0.01 (1% chance of having the disease = prior probability)
-
P(No Disease) = 0.99 (99% chance of not having the disease)
-
P(Positive Test | Disease) = 0.99 (99% true positive rate = likelihood)
-
P(Positive Test | No Disease) = 0.05 (5% false positive rate)
Step 2: Calculate the probability of a positive test result, P(PositiveTest)P(Positive Test)P(PositiveTest).
We use total probability to calculate this:
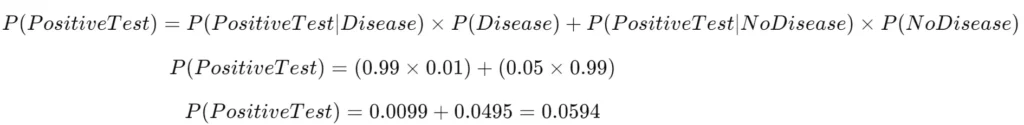
Step 3: Apply Bayes' Theorem.
Now, we can calculate the probability that you have the disease given a positive test result P(Disease∣PositiveTest)P(Disease | Positive Test)P(Disease∣PositiveTest):
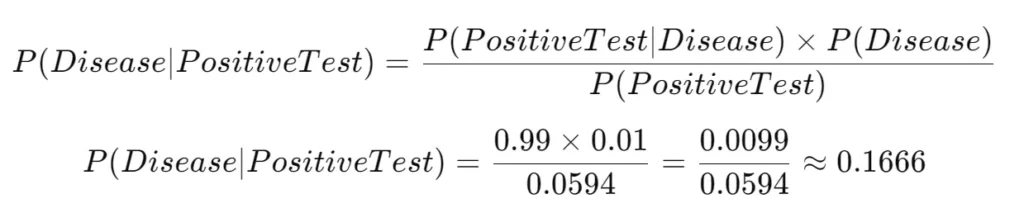
So, even with a positive test result, the probability that you actually have the disease is only 16.66%! 🤯
This result might be surprising, but it highlights how important prior probabilities (in this case, the rarity of the disease) are when interpreting test results. This is a key example of how Bayes’ theorem can be applied to medical diagnostics and shows why simply having a positive test result doesn’t guarantee you have a condition.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Real-World Applications of Bayes’ Theorem 🌍
Bayes’ theorem isn’t just confined to medical diagnostics. It’s a versatile tool used across various fields, including:
1. Spam Filtering 📧
Email providers use Bayes’ theorem to filter out spam by analyzing the likelihood that an email is spam based on certain words or patterns. If an email contains certain trigger words often associated with spam (like “free” or “urgent”), Bayesian spam filters will adjust the probability of the email being spam accordingly.
2. Machine Learning and AI 🤖
Bayesian networks are used in machine learning to predict future outcomes based on existing data. This approach is essential in systems that require continual learning and updating predictions based on new evidence, such as speech recognition, image classification, or self-driving cars.
3. Weather Forecasting 🌦️
Meteorologists use Bayes’ theorem to update predictions based on incoming data. For example, if radar indicates storm clouds moving into an area, the probability of rain increases. As more data comes in, the forecast is continually updated.
4. Legal Decision Making ⚖️
In legal cases, Bayes’ theorem can help calculate the likelihood of guilt or innocence based on prior evidence and newly presented facts. While controversial, this method is used in some forensic applications to weigh the likelihood of certain events based on available evidence.
5. Search Engines and Recommendation Systems 🔍
Search engines and recommendation algorithms use Bayes’ theorem to rank results. They calculate the likelihood that a specific link or item is relevant to the user based on previous searches and behaviors.
Bayesian Thinking: Updating Beliefs with New Evidence 🧠
One of the most powerful implications of Bayes’ theorem is the concept of Bayesian thinking—the idea that we should continuously update our beliefs as we receive new information.
Imagine you’re a detective investigating a crime. Initially, you might think Suspect A is the most likely culprit based on the evidence you have. However, as new information comes in, you revise your beliefs. Bayesian thinking helps you adjust your initial hypotheses based on new data, leading to better decision-making.
This principle can be applied to any decision-making process where uncertainty is involved, whether it’s investment strategies, medical treatments, or even day-to-day problem-solving.
Why Bayes’ Theorem is Important 🏅
Bayes’ theorem helps us make better decisions in situations of uncertainty by allowing us to factor in prior knowledge and new evidence. It gives us a structured way to update our beliefs and predictions based on the information available. This is why it’s so widely used in fields like medicine, machine learning, forensics, and everyday decision-making.
Understanding Bayes’ theorem equips us with the ability to think probabilistically, helping us navigate complex and uncertain situations with more clarity. It also emphasizes that new evidence should always be considered in the context of what we already know—this is critical for accurate reasoning.
Conclusion: Apply Bayes' Theorem to Everyday Decisions
Bayes’ theorem might seem abstract at first, but it’s an incredibly powerful tool that you can apply in everyday decision-making. From analyzing medical test results to deciding whether to carry an umbrella based on the weather forecast, the principles of conditional probability are all around us.
By understanding and applying Bayesian thinking, you’ll improve your ability to update your beliefs and make better decisions as new information becomes available.
Next time you’re faced with uncertainty, remember to use Bayes’ theorem to reassess the probabilities based on the evidence at hand. After all, in an uncertain world, the more you know, the better you can act! 📊🔍