The world of mathematics and physics is built upon a foundation of profound equations that have transformed our understanding of the universe. These equations are the cornerstones of various scientific fields, providing insights that have led to groundbreaking discoveries and technological advancements. In this blog – Foundational Equations in Mathematics and Physics, we delve into nine foundational equations, exploring their significance and applications. 📚🔍
1. Pythagorean Theorem (Geometry) 📐
Equation:

Description: This theorem, proposed by ancient Greek mathematician Pythagoras, relates the lengths of the sides of a right-angled triangle. It is a fundamental principle in Euclidean geometry and has been extensively used in various fields, including physics, computer graphics, and engineering design.
Key Applications:
- Engineering: Design and analysis of structures.
- Physics: Calculations involving vectors and forces.
Computer Graphics: Rendering 3D models and animations
2. Fourier Transform (Signal Processing) 📊
Equation:

Description: Developed by Joseph Fourier in the early 19th century, the Fourier Transform allows a mathematical function to be decomposed into its constituent frequencies. This technique is fundamental in the field of signal processing and has found applications in audio signal processing, image analysis, and solving partial differential equations.
Key Applications:
- Signal Processing: Audio and image compression.
- Physics: Analyzing waveforms and quantum mechanics.
Engineering: Telecommunications and control systems.
3. Einstein's Equation (Special Relativity) 🌌
Equation:
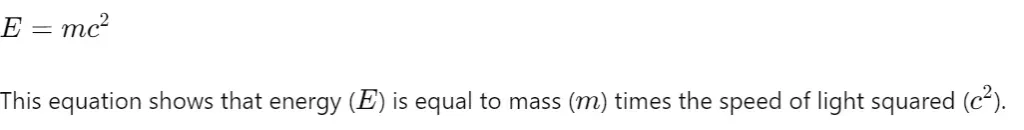
Description: This equation, E=mc2E=mc^2E=mc2, was derived by Albert Einstein as part of his theory of special relativity in 1905. It states that mass and energy are interchangeable, and this relationship has had a major impact on the development of nuclear energy and nuclear weapons.
Key Applications:
- Nuclear Physics: Understanding atomic reactions.
- Astrophysics: Studying cosmic phenomena.
- Energy Production: Nuclear power generation.
4. Heisenberg's Uncertainty Principle (Quantum Mechanics) 🌀
Equation:

Description: Formulated by Werner Heisenberg in 1927, the uncertainty principle is one of the core tenets of quantum mechanics. It states that the more precisely the position of a particle is determined, the less precisely its momentum can be known, and vice versa. This principle underpins the probabilistic nature of quantum mechanics.
Key Applications:
- Quantum Computing: Designing algorithms and hardware.
- Particle Physics: Studying subatomic particles.
- Cryptography: Quantum key distribution.
5. Dirac Equation (Quantum Field Theory) 🧲
Equation:

Description: Proposed by Paul Dirac in 1928, this equation describes fermions—particles with half-integer spin—and led to the prediction of antimatter. It’s critical in quantum field theory and has deepened our understanding of the behavior of subatomic particles and the universe.
Key Applications:
- Quantum Mechanics: Modeling particles.
- Astrophysics: Understanding black holes.
- Material Science: Developing new materials.
6. Euler’s Identity (Complex Analysis) 🧮
Equation:

Description: Named after the Swiss mathematician Leonhard Euler, this identity is a special case of Euler’s formula from complex analysis, and it beautifully combines five of the most important numbers in mathematics: eee, iii, π\piπ, 1, and 0. It is often cited as an example of mathematical beauty due to its elegant linking of these fundamental numbers.
Key Applications:
- Mathematics: Complex number theory.
- Physics: Quantum mechanics and wave equations.
- Engineering: Electrical engineering and signal processing.
7. Maxwell's Equations (Electrodynamics) ⚡
Equation:


Description: Formulated by James Clerk Maxwell in the 19th century, these four equations describe how electric and magnetic fields interact. They form the foundation of classical electrodynamics, optics, and electric circuits.
Key Applications:
- Electrical Engineering: Design of electrical circuits and systems.
- Telecommunications: Radio, television, and cell phone signals.
- Physics: Understanding electromagnetic waves.
8. Einstein’s Field Equations (General Relativity) 🌠
Equation:

Description: Published by Albert Einstein in 1915, these equations describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy. They are a cornerstone of modern physics and cosmology.
Key Applications:
- Cosmology: Understanding the universe’s structure.
- Astrophysics: Studying black holes and neutron stars.
- GPS Technology: Accurate positioning systems.
9. Schrödinger Equation (Quantum Mechanics) ⚛️
Equation:

Description: Proposed by Erwin Schrödinger in 1925, this equation describes how the quantum state of a physical system changes over time. It is a fundamental equation in quantum mechanics and underlies many modern technologies.
Key Applications:
- Quantum Mechanics: Describing the behavior of particles.
- Chemistry: Understanding molecular structures.
- Technology: Developing semiconductors and transistors.
Conclusion : Foundational Equations in Mathematics and Physics
These nine equations are more than just mathematical expressions; they are the keys to understanding the complexities of the universe. From the smallest particles to the vastness of space, these equations have paved the way for scientific discoveries and technological advancements. By exploring these foundational equations, we gain a deeper appreciation of the elegant laws that govern our world. 🌌


















